En la siguiente figura podemos observar la conexión de cuatro FF tipo J-K para formar un contador asíncrono de 4 BITS, comúnmente conocido como Contador de Rizo de 4 BITS.
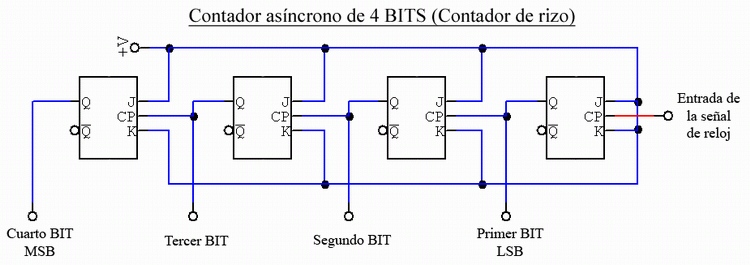Figura 1
El funcionamiento de este circuito se basa en cuatro puntos importantes:
Este diseño de contador, es conocido como "Contador Asíncrono", debido a que los cambios de estado en los FF son asíncronos con respecto a la señal de reloj, es decir, no ocurren al mismo tiempo que cambia la señal de reloj. El único que obedece directamente a los cambios de la señal de reloj es el primer FF.
Esta configuración nos permite observar que se produce un retraso en la propagación de la señal desde la entrada a la salida (Ya que existe un pequeño tiempo de retraso cuando un FF cambia de estado, el cuál explicaremos a detalle más adelante).
Este es el uno de los "defectos" de los contadores de rizo, debido al retraso explicado anteriormente, este tipo de contadores tiene un límite en la frecuencia de reloj aplicada a su entrada, aunque los retrasos en los FF modernos son muy pequeños (entre los 10 y los 40 nano-segundos), si se aplica a la entrada una frecuencia muy alta, el contador no puede funcionar de manera correcta.
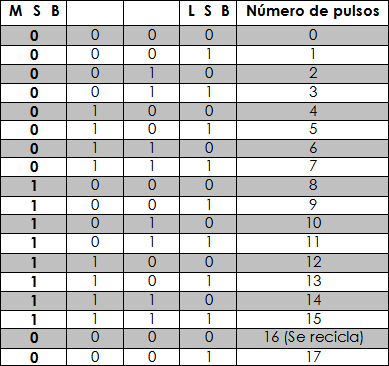
Tabla 1
Contadores asíncronos integrados en un solo chip.
Los ejemplos anteriores de circuitos discretos (todo hechos con FF) sólo son para ejemplificar la construcción del contador, en la práctica, son obsoletos ya que se necesitan muchos integrados y espacio para crearlos.
En el mercado podemos conseguir diferentes tipos de integrados con tecnología TTL o CMOS con contadores de rizo internos, Uno de los ejemplos más usados es el 74LS293.
En la figura 2, se encuentra el diagrama interno del integrado.
(Se toma por entendido que todas las entradas "J-K" están en estado ALTO)
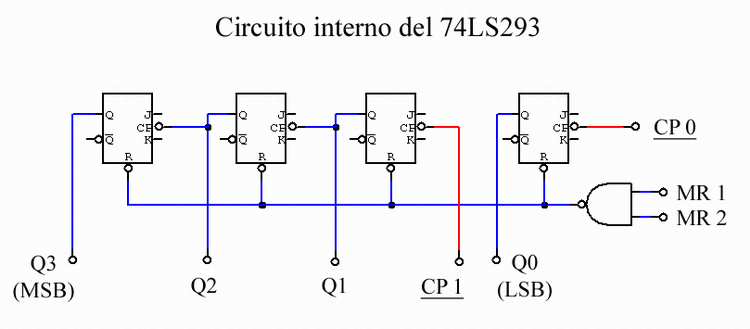
Figura 2
En este diagrama podemos observar una conexión muy parecida a la de la figura anterior, el integrado cuenta con cuatro FF tipo "J-K", cada una de las salidas de los FF representa un BIT, desde Q0 (LSB), hasta Q3 (MSB).
Cada uno de los FF cuenta con una entrada de reloj, pero en este caso, solamente dos son accesibles desde el exterior, la entrada del primer FF (CP 0), y la del segundo FF (CP 1), esta configuración nos permite utilizar los últimos tres FF como contador de tres bits y el primero por separado, o utilizar los cuatro bits para la cuenta.
Todos los FF cuentan con una entrada de RESET, la cual se encuentra conectada a una compuerta NAND de dos entradas, las cuáles son accesibles desde el exterior (MR 1 y MR 2), de esta manera se puede logra el reset del contador desde dos puntos diferentes.
Número MOD
En los casos anteriores, los dos contadores pueden darnos una salida de 4 BITS, es decir, cuentan desde el 0000 hasta el 1111, Para efectos prácticos, estos contadores son denominados Contadores "MOD 16", Ya que presentan 16 estados diferentes en la cuenta. Por lo que el número MOD, siempre es igual al número de estados que podemos obtener del contador antes que recicle su cuenta.
La siguiente tabla nos muestra los diferentes números MOD.
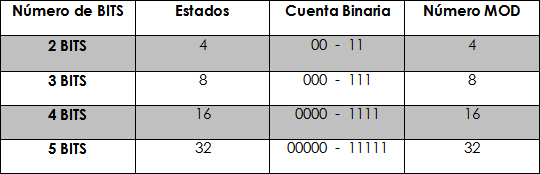
Tabla 2
Por lo que podemos observar en la relación de la tabla, al agregar un BIT más de cuenta (Otro FF), se duplica el número de estados posibles y por lo tanto también el número MOD.
Esto no permite llegar a una fórmula para saber cuál es el número MOD de un contador sabiendo el número de FF que se van a conectar.
Número MOD = 2 (N)
Lo que puede traducirse como "El número MOD es igual a 2 multiplicado a la (N) potencia". El número "N" es el número de FF que deseemos ocupar.
Por ejemplo, ¿cuál será el número MOD de un contador con 6 FF (6 BITS)?
Entonces: MOD = 2 (6)
MOD = 2 multiplicado a la sexta potencia
MOD = 2*2*2*2*2*2
MOD = 64
Contadores con Número MOD diferente a 2 (N)
En el ejemplo anterior pudimos encontrar el número MOD de un contador basado en la fórmula de 2 (N), pero:
¿Cómo encontrar el número de FF que se necesitan para un contador que no sea un MOD 4 o MOD 8?
Por ejemplo:
Si necesitáramos hacer un contador MOD 6. ¿Cómo podríamos lograr esto?
Debido a la naturaleza de los números binarios, no se puede lograr de manera "Común" un número MOD que es diferente a los obtenidos por medio de la fórmula anterior.
En estos casos, lo que hacemos es crear un contador con el número MOD más cercano hacia arriba, En este caso, el más cercano es el MOD 8. Y hacer que el contador omita los estados que no son necesarios.
Es decir:
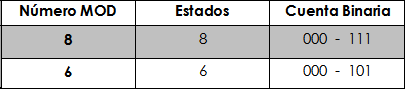
Tabla 3
La tabla nos muestra la cuenta máxima de un contador MOD 6, el cuál sería el número 5 (101), por lo que necesitamos hacer que nuestro contador "recicle" su cuenta al pasar de este número al siguiente.
En la siguiente figura, se representa el diagrama del contador que necesitamos.
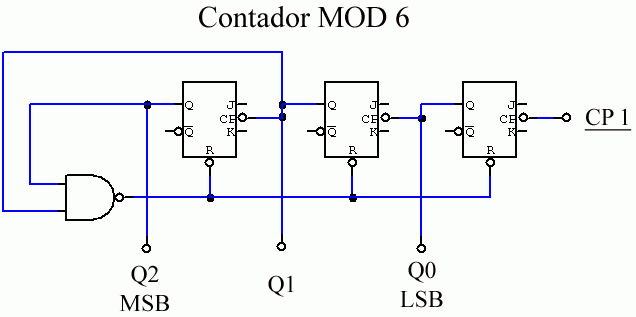
Figura 3
El funcionamiento de este circuito es básicamente el mismo que hemos visto hasta ahora, pero al agregar una compuerta NAND como control de las entradas de RESET, podemos hacer que nuestro contador se recicle al llegar al número que deseemos.
Cada una de las entradas está conectada a la salida de un FF, dependiendo de cuáles BITS sea, la compuerta ordenará el RESET a todos los FF, enviando la cuenta a cero o "reciclándola".
En este caso, una de las entradas de la compuerta NAND está conectada a la salida Q1 (Segundo BIT), y la otra a Q2 (Tercer BIT), por lo que solamente habrá un pulso de RESET a la salida en la compuerta cuando sus dos entradas se encuentren en el estado ALTO. Por lo que la compuerta actuará cuando esté presente el número seis (110), enviando la cuenta nuevamente a cero (000).
Al ser un contador de rizo, nuevamente nos topamos con el factor del retraso en la propagación de la cuenta, ya que se necesita cierto tiempo para que la señal de salida de los contadores sea enviada al RESET de los FF, por un pequeño momento (tal vez no perceptible para nosotros), será visible el número 6, e inmediatamente será reciclado a cero. Este efecto es claramente visible si a nuestro contador le incorporamos un decodificador de Código Binario a un display de 7 segmentos y ocupamos una frecuencia de reloj muy baja.
El retraso en la propagación de la cuenta es la causa principal por la que los contadores de rizo no son muy utilizados en sistemas de medición de tiempo. Por ejemplo un reloj digital, ya que después de cierto tiempo, el reloj quedará retrasado.
Dirección de la cuenta en los contadores de rizo.
Hasta ahora sólo hemos visto contadores asíncronos que siempre elevan el número de la cuenta, pero ¿Cómo lograr que el contador funcione restando la cuenta? La solución es muy sencilla, simplemente se alimentan los FF con las salidas Negadas o Invertidas de los FF, no importa el número MOD de un contador, si se toman las salidas Negadas como reloj para los siguientes FF, la cuenta siempre será hacia abajo.
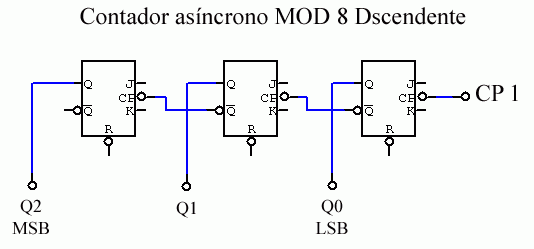
Figura 4
El funcionamiento de este circuito se basa en cuatro puntos importantes:
- ALos pulsos de reloj sólo son aplicados a la entrada CP (Clock, reloj) del primer Fip-Flop. Teniendo en cuenta que es un FF tipo "J-K", y que estas dos entradas se encuentran en un nivel alto (Conectadas a V+), el FF realizará la función de complemento o "Toggle", conmutando sus salidas con cada pulso de la señal de reloj. El cambio puede ser controlado por transiciones positivas o negativas de la señal de reloj, esto depende únicamente del tipo de entrada del FF.
- La salida del primer FF (Primer BIT) actúa como pulso de reloj para el siguiente FF (Segundo BIT), y así sucesivamente hasta llegar al cuarto FF. De esta manera se logra que un FF sólo pueda cambiar de estado cuando el anterior le proporcione la transición correcta a su entrada.
- Las salidas de los FF representan el número binario de 4 BITS, Obteniendo del primer FF el LSB (Dígito menos significativo), y del último el MSB (Dígito más significativo). Al comenzar la cuenta, teóricamente las salidas de los FF deben estar en cero, esto nos da e número 0000, esto puede lograrse con las entradas de "Restablecer" (RESET), las cuáles no son mostradas en el diagrama. La tabla 1, muestra la secuencia de conteo desde el número 0000 al 1111.
- Una vez que ha llegado el quinceavo pulso de entrada, el contador se encontrará en la cuenta máxima para 4 BITS, es decir 1111, al llegar el siguiente pulso, el contador volverá a la posición original de 0000, Esto supone un ciclo completo del contador y se conoce como el "reciclado" de la cuenta.
Este diseño de contador, es conocido como "Contador Asíncrono", debido a que los cambios de estado en los FF son asíncronos con respecto a la señal de reloj, es decir, no ocurren al mismo tiempo que cambia la señal de reloj. El único que obedece directamente a los cambios de la señal de reloj es el primer FF.
- Cambio del primer FF = Señal de reloj
- Cambio del segundo FF = Primer FF + Señal de reloj
- Cambio del tercer FF = Segundo FF + Primer FF + Señal de reloj
- Cambio del cuarto FF = Tercer FF + Segundo FF + Primer FF + Señal de reloj.
Esta configuración nos permite observar que se produce un retraso en la propagación de la señal desde la entrada a la salida (Ya que existe un pequeño tiempo de retraso cuando un FF cambia de estado, el cuál explicaremos a detalle más adelante).
Este es el uno de los "defectos" de los contadores de rizo, debido al retraso explicado anteriormente, este tipo de contadores tiene un límite en la frecuencia de reloj aplicada a su entrada, aunque los retrasos en los FF modernos son muy pequeños (entre los 10 y los 40 nano-segundos), si se aplica a la entrada una frecuencia muy alta, el contador no puede funcionar de manera correcta.
Tabla 1
Contadores asíncronos integrados en un solo chip.
Los ejemplos anteriores de circuitos discretos (todo hechos con FF) sólo son para ejemplificar la construcción del contador, en la práctica, son obsoletos ya que se necesitan muchos integrados y espacio para crearlos.
En el mercado podemos conseguir diferentes tipos de integrados con tecnología TTL o CMOS con contadores de rizo internos, Uno de los ejemplos más usados es el 74LS293.
En la figura 2, se encuentra el diagrama interno del integrado.
(Se toma por entendido que todas las entradas "J-K" están en estado ALTO)
Figura 2
En este diagrama podemos observar una conexión muy parecida a la de la figura anterior, el integrado cuenta con cuatro FF tipo "J-K", cada una de las salidas de los FF representa un BIT, desde Q0 (LSB), hasta Q3 (MSB).
Cada uno de los FF cuenta con una entrada de reloj, pero en este caso, solamente dos son accesibles desde el exterior, la entrada del primer FF (CP 0), y la del segundo FF (CP 1), esta configuración nos permite utilizar los últimos tres FF como contador de tres bits y el primero por separado, o utilizar los cuatro bits para la cuenta.
Todos los FF cuentan con una entrada de RESET, la cual se encuentra conectada a una compuerta NAND de dos entradas, las cuáles son accesibles desde el exterior (MR 1 y MR 2), de esta manera se puede logra el reset del contador desde dos puntos diferentes.
Número MOD
En los casos anteriores, los dos contadores pueden darnos una salida de 4 BITS, es decir, cuentan desde el 0000 hasta el 1111, Para efectos prácticos, estos contadores son denominados Contadores "MOD 16", Ya que presentan 16 estados diferentes en la cuenta. Por lo que el número MOD, siempre es igual al número de estados que podemos obtener del contador antes que recicle su cuenta.
La siguiente tabla nos muestra los diferentes números MOD.
Tabla 2
Por lo que podemos observar en la relación de la tabla, al agregar un BIT más de cuenta (Otro FF), se duplica el número de estados posibles y por lo tanto también el número MOD.
Esto no permite llegar a una fórmula para saber cuál es el número MOD de un contador sabiendo el número de FF que se van a conectar.
Número MOD = 2 (N)
Lo que puede traducirse como "El número MOD es igual a 2 multiplicado a la (N) potencia". El número "N" es el número de FF que deseemos ocupar.
Por ejemplo, ¿cuál será el número MOD de un contador con 6 FF (6 BITS)?
Entonces: MOD = 2 (6)
MOD = 2 multiplicado a la sexta potencia
MOD = 2*2*2*2*2*2
MOD = 64
Contadores con Número MOD diferente a 2 (N)
En el ejemplo anterior pudimos encontrar el número MOD de un contador basado en la fórmula de 2 (N), pero:
¿Cómo encontrar el número de FF que se necesitan para un contador que no sea un MOD 4 o MOD 8?
Por ejemplo:
Si necesitáramos hacer un contador MOD 6. ¿Cómo podríamos lograr esto?
Debido a la naturaleza de los números binarios, no se puede lograr de manera "Común" un número MOD que es diferente a los obtenidos por medio de la fórmula anterior.
En estos casos, lo que hacemos es crear un contador con el número MOD más cercano hacia arriba, En este caso, el más cercano es el MOD 8. Y hacer que el contador omita los estados que no son necesarios.
Es decir:
Tabla 3
La tabla nos muestra la cuenta máxima de un contador MOD 6, el cuál sería el número 5 (101), por lo que necesitamos hacer que nuestro contador "recicle" su cuenta al pasar de este número al siguiente.
En la siguiente figura, se representa el diagrama del contador que necesitamos.
Figura 3
El funcionamiento de este circuito es básicamente el mismo que hemos visto hasta ahora, pero al agregar una compuerta NAND como control de las entradas de RESET, podemos hacer que nuestro contador se recicle al llegar al número que deseemos.
Cada una de las entradas está conectada a la salida de un FF, dependiendo de cuáles BITS sea, la compuerta ordenará el RESET a todos los FF, enviando la cuenta a cero o "reciclándola".
En este caso, una de las entradas de la compuerta NAND está conectada a la salida Q1 (Segundo BIT), y la otra a Q2 (Tercer BIT), por lo que solamente habrá un pulso de RESET a la salida en la compuerta cuando sus dos entradas se encuentren en el estado ALTO. Por lo que la compuerta actuará cuando esté presente el número seis (110), enviando la cuenta nuevamente a cero (000).
Al ser un contador de rizo, nuevamente nos topamos con el factor del retraso en la propagación de la cuenta, ya que se necesita cierto tiempo para que la señal de salida de los contadores sea enviada al RESET de los FF, por un pequeño momento (tal vez no perceptible para nosotros), será visible el número 6, e inmediatamente será reciclado a cero. Este efecto es claramente visible si a nuestro contador le incorporamos un decodificador de Código Binario a un display de 7 segmentos y ocupamos una frecuencia de reloj muy baja.
El retraso en la propagación de la cuenta es la causa principal por la que los contadores de rizo no son muy utilizados en sistemas de medición de tiempo. Por ejemplo un reloj digital, ya que después de cierto tiempo, el reloj quedará retrasado.
Dirección de la cuenta en los contadores de rizo.
Hasta ahora sólo hemos visto contadores asíncronos que siempre elevan el número de la cuenta, pero ¿Cómo lograr que el contador funcione restando la cuenta? La solución es muy sencilla, simplemente se alimentan los FF con las salidas Negadas o Invertidas de los FF, no importa el número MOD de un contador, si se toman las salidas Negadas como reloj para los siguientes FF, la cuenta siempre será hacia abajo.
Figura 4
