Dr. Zoidberg
Well-known-Papá Pitufo
Este tema tal vez debería ir en pequeña señal (o en radio  ), pero lo inicio acá por que está pensado para el cálculo de los filtros LC en los amplificadores clase D.
), pero lo inicio acá por que está pensado para el cálculo de los filtros LC en los amplificadores clase D.
Bueno, un filtro LC es un filtro, al menos, de segundo orden, cuando consta de un inductor L y de un capacitor C, tales como los que están usando hasta ahora, aunque el orden puede ser mayor si aumentamos la cantidad de componentes L y C.
En un amplificador tipo UCD no tiene mucho caso aumentar el orden del filtro, por que el mismo está dentro del lazo de realimentación del amplificador, y cualquier cambio alteraría dramáticamente la dinámica del lazo. Sin embargo, en un amplificador tipo NO-UCD, como el Sorenson del Ing. Tagle es factible aumentar el orden del filtro ya que el mismo no se encuentra encerrado en el lazo de realimentación y mejorar el rechazo a la "portadora".
Bien, la idea ahora es diseñar un filtro pasa-bajos de segundo orden siguiendo una metodología ordenada y que responda a la teoría de los filtros. Demás está decir que para tener toda la información necesaria van a necesitar un libro sobre filtros, aunque en este tema les voy a subir una tabla solo para filtros Butterworth, pero como eso es propiedad de los autores del libro...los dejo a ustedes conseguirlo. El que he usado en este tema es "Analog and Digital Filter Design (2nd ed)" de Steve Winder y es un libro muy "accesible".
Primero veamos la estructura general del filtro LC.
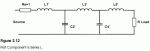
Sabiendo que vamos a calcular un filtro de Butterworth (respuesta en frecuencia máximamente plana --> bueno para audio), a continuación les muestro una tabla que contiene los coeficientes normalizados de los filtros de Butterworth hasta de orden 10.

Fíjense que en el esquema se han considerado los componentes con nombre Li' y Ci', que en la tabla corresponden a la fila con Rs=0, cuando en el esquema aparece normalizada para Rs=1. Esto se debe a que la tabla está construida para estructuras de filtrado donde la resistencia de la fuente de señal (Rs=resistencia de salida del amplificador) es mucho menor que la resistencia de carga, cosa que sucede en los amplificadores de audio.
Como verán, con solo saber el orden del filtro que tengo que construir es fácil darle valores a los componentes L y C, ya que los sacamos de la tabla. El problema es que estos valores están dados para una frecuencia de corte de 1 Rad/s y para una resistencia de carga de 1 ohm, así que hay que escalarlos a nuestra necesidad: por ejemplo una frecuencia de corte de 30 kHz y una impedancia de carga de 8 ohms.
Para eso, usamos la figura que viene a continuación:

Con esas ecuaciones que están ahí y los valores de nuestra aplicación (Fc= frecuencia de corte y R= resistencia de carga) es muy simple obtener los valores finales que tomarán los componentes L y C.
Hagamos un ejemplo:
Calcular un filtro pasabajos LC de segundo orden con Fc=30kHz y R=8 ohms.
De la tabla, para orden=2, sacamos: L* = 1.41422 y C* = 0.70711
Reemplazando en las ecuaciones de arriba y usando la calculadora tenemos:
tenemos:
L1 = (8 * 1.41422) / (2 * PI * 30000) = 60 uHy
C2 = 0.70711 / ( 2 * PI * 8 * 30000) = 470nF
Si nos dieran valores de C que no estuvieran normalizados, podriamos multiplicar y dividir por alguna constante para llevar los valores a algo mas comercial, aunque los valores obtenidos acá son los que mejor se ajustan a la impedancia de carga. Por ejemplo, si tenemos un capacitor de poliester de 1.5uF podríamos hacer:
C2= 1.5uF
k=1.5 / 0.47 = 3.19
L1 = 60uHy / k = 18.8 uHy
Fácil, eh?
Bueno, esto que hemos hecho para un filtro LC de orden 2 es lo forma correcta de considerar los efectos en el filtro de la impedancia de carga.
Si en lugar de usar un filtro de Butterworth quieren usar uno de Bessel o uno de Chebyschev, pues solo tienen que cambiar de tabla y listo, el resto es igual. Lo mismo que si quieren hacer filtros de orden mas elevado...solo hay que tomar los valores de la fila correspondiente al orden deseado.
Espero que les sea de utilidad.
Bueno, un filtro LC es un filtro, al menos, de segundo orden, cuando consta de un inductor L y de un capacitor C, tales como los que están usando hasta ahora, aunque el orden puede ser mayor si aumentamos la cantidad de componentes L y C.
En un amplificador tipo UCD no tiene mucho caso aumentar el orden del filtro, por que el mismo está dentro del lazo de realimentación del amplificador, y cualquier cambio alteraría dramáticamente la dinámica del lazo. Sin embargo, en un amplificador tipo NO-UCD, como el Sorenson del Ing. Tagle es factible aumentar el orden del filtro ya que el mismo no se encuentra encerrado en el lazo de realimentación y mejorar el rechazo a la "portadora".
Bien, la idea ahora es diseñar un filtro pasa-bajos de segundo orden siguiendo una metodología ordenada y que responda a la teoría de los filtros. Demás está decir que para tener toda la información necesaria van a necesitar un libro sobre filtros, aunque en este tema les voy a subir una tabla solo para filtros Butterworth, pero como eso es propiedad de los autores del libro...los dejo a ustedes conseguirlo. El que he usado en este tema es "Analog and Digital Filter Design (2nd ed)" de Steve Winder y es un libro muy "accesible".
Primero veamos la estructura general del filtro LC.

Sabiendo que vamos a calcular un filtro de Butterworth (respuesta en frecuencia máximamente plana --> bueno para audio), a continuación les muestro una tabla que contiene los coeficientes normalizados de los filtros de Butterworth hasta de orden 10.

Fíjense que en el esquema se han considerado los componentes con nombre Li' y Ci', que en la tabla corresponden a la fila con Rs=0, cuando en el esquema aparece normalizada para Rs=1. Esto se debe a que la tabla está construida para estructuras de filtrado donde la resistencia de la fuente de señal (Rs=resistencia de salida del amplificador) es mucho menor que la resistencia de carga, cosa que sucede en los amplificadores de audio.
Como verán, con solo saber el orden del filtro que tengo que construir es fácil darle valores a los componentes L y C, ya que los sacamos de la tabla. El problema es que estos valores están dados para una frecuencia de corte de 1 Rad/s y para una resistencia de carga de 1 ohm, así que hay que escalarlos a nuestra necesidad: por ejemplo una frecuencia de corte de 30 kHz y una impedancia de carga de 8 ohms.
Para eso, usamos la figura que viene a continuación:

Con esas ecuaciones que están ahí y los valores de nuestra aplicación (Fc= frecuencia de corte y R= resistencia de carga) es muy simple obtener los valores finales que tomarán los componentes L y C.
Hagamos un ejemplo:
Calcular un filtro pasabajos LC de segundo orden con Fc=30kHz y R=8 ohms.
De la tabla, para orden=2, sacamos: L* = 1.41422 y C* = 0.70711
Reemplazando en las ecuaciones de arriba y usando la calculadora
L1 = (8 * 1.41422) / (2 * PI * 30000) = 60 uHy
C2 = 0.70711 / ( 2 * PI * 8 * 30000) = 470nF
Si nos dieran valores de C que no estuvieran normalizados, podriamos multiplicar y dividir por alguna constante para llevar los valores a algo mas comercial, aunque los valores obtenidos acá son los que mejor se ajustan a la impedancia de carga. Por ejemplo, si tenemos un capacitor de poliester de 1.5uF podríamos hacer:
C2= 1.5uF
k=1.5 / 0.47 = 3.19
L1 = 60uHy / k = 18.8 uHy
Fácil, eh?
Bueno, esto que hemos hecho para un filtro LC de orden 2 es lo forma correcta de considerar los efectos en el filtro de la impedancia de carga.
Si en lugar de usar un filtro de Butterworth quieren usar uno de Bessel o uno de Chebyschev, pues solo tienen que cambiar de tabla y listo, el resto es igual. Lo mismo que si quieren hacer filtros de orden mas elevado...solo hay que tomar los valores de la fila correspondiente al orden deseado.
Espero que les sea de utilidad.
Última edición:




