Continuando desde el mensaje # 1
CÁLCULOS TRANSFORMADOR DE SALIDA DE AUDIO Hi-Fi
Para amplificador de 20 W R.M.S., Push-Pull Paralelo, Clase A, para 2 dobles triodos de potencia 6AS7
Núcleo Acorazado
EI
Laminación 155, 38 mm de rama central, grano orientado (G.O.) M4 (0,27 mm).
Longitud media magnética
(lmmg) laminación 155 : 24,7 cm
Potencia
(W): 20 Watts R.M.S.
Respuesta de Frecuencia mínima a reproducir
(Fm): 20 Hz
Tensión efectiva de placas
(Eb): 250 VCC
Resistencia (impedancia) de carga de Placa a Placa
(Raa) (Z): 2500 Ω
Bobinado Primario
(N1) con punto medio
(p.m.)
Bobinado Secundario
(N2) para impedancia de bobina móvil
(Z´): 8 Ω
Cálculo de la sección del núcleo (S)
Para obtener la sección del núcleo utilizo la fórmula simplificada para transformadores de audio, extraída del libro “Transformadores” del Ing. F. L. Singer.
En la fórmula se pueden utilizar los coeficientes 10, o 15.
El coeficiente 10 se aplica para salidas push-pull clase A, donde las válvulas de potencia estén perfectamente apareadas (difícil de conseguir), y los semi-primarios del transformador de salida estén eléctricamente equilibrados, de esta manera se consigue que no circule la componente de continua, y se asegura que el núcleo no se sature.
El coeficiente 15 se aplica para salidas push-pull clases AB1, AB2, y B, donde más allá del apareamiento de las válvulas de salida, y los semi primarios equilibrados, se debe compensar la componente de continua, que sí circulará en los momentos en que una de las válvulas de salida esté en el corte, y la otra no, asegurándose también la no saturación del núcleo.
Aunque estos transformadores serán para un amplificador push-pull clase A, he elegido el coeficiente 15, dado que como nunca se logra un apareamiento perfecto de las válvulas de salida, me aseguro que en ningún momento circule corriente continua.
S= 15 x √Fm/W = 15 x √20 Hz/20 W= 15 cm2
S: 15 cm2
A este resultado debemos agregarle un 9% por factor de apilamiento, y aislación de las chapas, (15 x 9) / 100 = 1,35
S= 15 cm2 + 1,35 cm2 = 16,35 cm2
S: 16,35 cm2
Se empleará un carrete de plástico (hasta 130ºC), de 38mm x 43 mm, con separación 50%/50%.
Las fórmulas que se describen en el libro “Transformadores” del Ing. F. L. Singer son generosas, y no fallan nunca.
Realizaré una fórmula de otro autor para hallar la sección del núcleo al mero hecho didáctico, y comparativo.
Hallaremos la sección del núcleo
(S), utilizando el método descripto por Giunchi Fabrizio, publicado en su libro “Manuale per il calcolo di trasformatori” (año 2014).
En este caso para hallar la sección del núcleo
(S), se parte de la superficie en cm2 (A x B) de una laminación EI, donde A es el largo de la E, y B es el ancho de la E, no se cuenta la superficie de la I, porque es igual a la suma de las superficies de las dos ventanas de la E.
A x B = 100 x √P/B x Fm = cm2 = 100 x √20 W / 0,8 T x 20 Hz = 112 cm2
La laminación existente cuya superficie (A x B) es la más aproximada por exceso al resultado de 112 cm2 es la laminación 60, cuya superficie (A x B) es de 120 cm2 (7% mayor), y su rama central de 4 cm, y la más aproximada por defecto es la laminación 155, cuya superficie (A x B) es de 108,3 cm2 (3,4% menor), y su rama central de 3,8 cm.
Pero como esto es una comparación, imaginemos para el cálculo de la sección, una laminación a medida que de aproximadamente 112 cm2, calculando, sería de 3,85 cm de rama central, y con este dato, su superficie (A x B) es de 111,17 cm2 (0,75% menor) valor ahora bastante aproximado.
Entonces :
Fórmula sección del núcleo
(S):
S = C ^ 2 / Fap = cm2
Donde C es la medida de la rama central de una laminación EI, y Fap es el factor de apilamiento.
Rama central de la laminación creada: 3,85 cm.
Fap : 1,11 (factor de apilamiento que utiliza Giunchi Fabrizio)
S = C ^2 / Fap = cm2
S= 3,85 ^2 /1,11=
13,35 cm2
Comparando los dos resultados, la fórmula de Giunchi Fabrizio que da una sección del núcleo (S) de 13,35 cm2, es 12% menor con respecto a la fórmula del Ing. F. L. Singer que da una sección de 15 cm2.
Cálculo del número de espiras del bobinado Primario
Por motivos didácticos, y comparativos que anteriormente les mencioné, emplearemos fórmulas de cuatro autores, vamos a ver más adelante, que la fórmula más generosa es la del Ing. F. L. Singer, sin embargo, y debido a que en este transformador, su bobinado primario será dividido en 10 galletas, su bobinado secundario en 8 galletas, y todas intercaladas, donde también deben quedar las capas de los bobinados lo más completa posible, y caber todo dentro de las ventanas, hace que se tengan que manipular dentro de un margen razonable ciertos resultados.
Para las 4 fórmulas siguientes se usará para la sección del núcleo (S) el resultado de la fórmula del Ing. F. L. Singer: S = 15 cm
De las 4 fórmulas, en las tres siguientes, se usará una inducción
(B) fijada en 8.000 gauss, tal cual usan los autores, donde generalmente se emplea para laminaciones de calidad estándar, grano no orientado (G.N.O.)
Fórmula del número de espiras del primario, publicada en su libro por el Ing. F. L. Singer
Nº espiras del Primario = 0,315 x Eb x 10^8 / B x Fm x S
0,315 x 250 VCC x 10^8 / 8.000 Gauss x 20 Hz x 15 cm2 =
3.281 espiras
2)Fórmula del número de espiras del bobinado primario, según Robert G. Wolpert en su libro “Audio Transformer Design Manual” https://es.scribd.com/document/312544651/Audio-Transformer-Design-Manual-Robert-G-Wolpert-2004
Nº de espiras del bobinado primario =
Eb x 10^8 / 4,44 x S (en pulgadas2) x Fm x B (en líneas por pulgada2)
Factor de conversión entre pulgada2, y cm2 = 6,45
S: 15 cm2 a pulgada2 = 15 cm2 / 6,45 = 2,33 pulgadas2
B: 8.000 Gauss a líneas por pulgada2 = 8.000 x 6,45 = 51.600 líneas por pulgada2
Nº de espiras = 250 VCC x 10^8 X 4,44 x 2,33 x 20 Hz x 51600:
2.342 espiras.
3)Fórmula del número de espiras del bobinado primario según Giunchi Fabrizio, publicada en su libro “ Manuale per il colcolo di Trasformatori” : https://www.audiovalvole.it/pdf/Manuale_Trasformatori.pdf
Voltios por espira
(Ve) = 4,44 x Fm x S x B (en Tesla) x 10^-4
10.000 Gauss = 1 Tesla (1 T)
8.000 gauss = 0,8 T
Voltios por espira
(Ve) = 4,44 x 20 Hz x 15 cm2 x 0,8 T x 10^-4 = 0,1066 Voltios por espira.
Nº de espiras = Eb / Ve = 250 Vcc / 0,1066 Voltios por espiras =
2.345 espiras.
Podrán apreciar que las 3 formulas vistas parten de la expresión general de la f.e.m. : E = 4,44 x F x B x S x N x 10^-8
4)Fórmula del número de espiras del Primario publicada por Grzegorz Makarewicz, de la página polaca Trioda: https://trioda.com/index.php/en/articles/radioamator-i-krotkofalowiec/4323-projektowanie-transformatorow-wyjsciowych-gb
En este caso, primero hay que hallar la inductancia del bobinado primario (L1), utilizando la siguiente fórmula:
L1= Raa / 2 x π x Fm
L1= 2.500 Ω / 2 x 3,14 x 20 Hz= 19,90 Hy
L1 : 19,90 Hy
Hallado el valor de la inductancia del bobinado primario, lo aplicamos a la siguiente fórmula para hallar el número de espiras.
Nº de espiras del bobinado Primario= 9.000 x (√L1 x lmmg / u x S)
Donde lmmg, es la longitud media magnética, que para la laminación 155 es de 24,7 cm, y donde u es la permeabilidad magnética del núcleo, de la cual se asume un valor medio de 500.
9.000 x (√19,90 Hy x 24,7 cm / 500 x 15 cm2)=
2.304 espiras
Entonces:
Nº de espiras según fórmula nº 1 del Ing. F. L. Singer: 3.281
Nº de espiras según fórmula nº2 de R. G. Wolpert : 2.342
Nº de espiras según fórmula nº3 de Giunchi Fabrizio : 2.345
Nº de espiras según fórmula nº4 de G. Makarewicz : 2.304
En las fórmulas nº 2, 3, y 4 los resultados del Nº de espiras son más, o menos similares.
Se aprecia que la fórmula nº 1 del Ing. Singer es la que arroja mayor cantidad espiras, y es 40% mayor que el promedio de las 3 fórmulas restantes, estaría bien elegir el resultado de esta fórmula.
Pero…..
Si utilizara la fórmula nº 1 del Ing. Singer (3281 espiras), no entrarían los bobinados del primario, y del secundario en las ventanas de la laminación 155 que decidí utilizar, con esta laminación, y 15 cm2 de núcleo, el transformador será bastante voluminoso, cambiar por una laminación más grande ha quedado descartado.
Así que utilizaré la misma fórmula nº1 del Ing. Singer, pero aumentando la inducción (B) de 8.000 Gauss a 9.350 Gauss, dado que no habrá inconvenientes por que se usará para el núcleo, laminación de grano orientado (G.O.).
Veamos:
Nº espiras del Primario = 0,315 x Eb x 10^8 / B x Fm x S
0,315 x 250 VCC x 10^8 / 9.350 Gauss x 20 Hz x 15 cm2 =
2.808 espiras.
Ahora si con este número caben todos los bobinados.
Se habrán dado cuenta que les escribo con el diario del lunes, así que para que todo quede bien proporcionado, (las espiras justas por capas, y cantidad de capas), hay que sumar 8 espiras más al bobinado primario.
2.808 + 8 = 2.816 espiras
Nº de espiras Bobinado Primario
N1 =
2816 espiras
Calculemos ahora el diámetro del alambre de cobre esmaltado para el bobinado primario, para ello se necesita saber cuánta corriente circulará por el bobinado primario N1.
La válvula 6AS7 es un doble triodo de potencia, donde la corriente placa de cada triodo es de 0,05 A, y como esta disposición es un Push-Pull Paralelo, se conecta en cada una de las dos 6AS7 sus dos triodos en paralelo, de esta manera la corriente de placa es de 0,1 A por cada una de las dos válvulas.
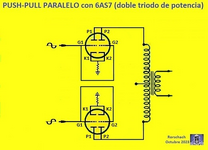
Entonces la corriente máxima circulante es de 0,1 A entre el punto medio (+B) y por cada una de las dos ramas del bobinado primario.
Sin embargo, por seguridad, y para que la resistencia óhmica del bobinado primario sea lo más baja posible, se hará el cálculo como si circulara un 60 % más de corriente por rama, o sea 0,16 A.
Usaremos una densidad de corriente de 2 A / mm2
La sección del alambre es: 0,16 A /2 A/mm2 = 0,08 mm2
Su diámetro es : 2 x √sección/π : 2 x √ 0,1 mm2 / π =
0,32 mm
Cálculo del número de espiras del bobinado Secundario N2
Para conectar a una bobina móvil de 8 Ω
Para determinar el número de espiras del secundario antes debemos saber cuál es la relación de transformación
(k).
K = √ Z / Z´ = √ 2500 Ω / 8 Ω =
17,678
Nº de espiras del bobinado Secundario
N2 =
N1 / k = 2816 / 17,678 = 159 espiras, redondeamos
160 espiras
Calculemos la máxima corriente que circulará por este Secundario :
Si para 8 Ω de impedancia nominal, se calcula +- 6,3 Ω de resistencia D.C., tomaremos este valor para mayor seguridad.
I = √ W / R = √ 20 W / 6,3 Ω = 1,78 A
Para el bobinado secundario tomaremos una densidad de corriente de 4 A / mm2.
1,78 A / 4 A /mm2 = 0,445 mm2 sección
Sección 0,445 mm2 a diámetro : 2 x √sección/π : 0,75 mm
Diámetro: 0,75 mm
Pero como se debe reducir la altura del bobinado, emplearé en el secundario 2 alambres en paralelo, de menor diámetro, y cuyo suma de secciones sea igual, o ligeramente mayor a un solo alambre.
Sección : 0,445 / 2 : 0,2225 mm2
2 alambres en paralelo: 0,2225 mm2 c/u
Sección 0,2225 mm2 a diámetro : 2 x √sección/π : 0,53 mm :
0,55 mm.
Entonces se empleará 2 alambres en paralelo de 0,55 mm de diámetro.-
Datos definitivos, y prácticos del transformador:
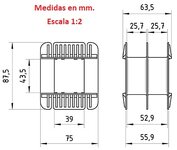
Sección del núcleo (S): 15 cm2 (16,35 mm2 incluyendo factor de apilamiento).
Laminación: EI nº 155, 38 mm de rama central, grano orientado M4 (0,27mm).
Carrete: plástico de 38 mm por 43 mm, con separación 50%/50%.
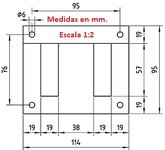
Nº de espiras del bobinado Primario: 2816
Cantidad de galletas bobinado Primario: “10” (ver gráfico: cantidad de espiras por galleta, cantidad de capas por galleta, y cantidad de espiras por capa).
Diámetro alambre de cobre esmaltado para el bobinado Primario: 0,32 mm.
Nº de espiras del bobinado Secundario: 160
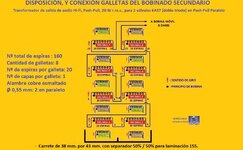
Cantidad de galletas bobinado Secundario: “8” (ver gráfico: cantidad de espiras por galleta, cantidad de capas por galleta, y cantidad de espiras por capa).
Diámetro alambre de cobre esmaltado para el bobinado Secundario: 0,55 mm (2 en paralelo)
Detalles Constructivos:
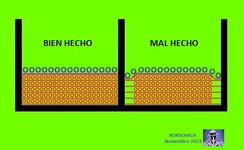
El bobinado primario se dividirá en 10 galletas, y el bobinado secundario en 8 galletas, todas ellas intercaladas, y aisladas según se muestra en el siguiente gráfico:


A continuación, disposición, y conexionado de las galletas del bobinado Secundario con todos los datos necesarios :
De aquí en más, solo falta construirlo, a medida del avance iré publicando.
Esto continúa.......

Saludos Cordiales
Rorschach