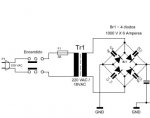
Buscando cosas por ahí, encontré una fórmula práctica para calcular los capacitores de filtro de una fuente de alimentación. La ecuación es la siguiente:
[LATEX]Vpp=\frac{I * \delta t * 1000} {C}[/LATEX]
Donde
[LATEX]Vpp[/LATEX] es la tensión de ripple pico-a-pico a la salida del filtro.
[LATEX]I[/LATEX] es la corriente de salida de la fuente dada en
Amperes.
[LATEX]\delta t[/LATEX] es el tiempo de descarga de los condensadores del filtro dado en
milisegundos, y vale
7 para 50Hz y
5.8 para 60Hz (en realidad son 100Hz y 120Hz que es la frecuencia del ripple, pero se entiende la idea, no?)
[LATEX]C[/LATEX] es el valor
TOTAL de la capacidad del filtro dado en
microfaradios.
Y el 1000 es para que quede bien puesto el punto decimal.
Esa ecuación surge de aproximar la forma exponencial decreciente de la descarga del condensador de filtro a un segmento de recta (su voltaje entre placas). Simplifica los cálculos enoooormemente. La premisa para emplearla es que la carga no sea compleja (debe ser resistiva pura) y no varíe su consumo (A) con un voltaje aplicado variable, pero lamentablemente no es el caso más frecuente de tener como carga (la carga debe ser un sink o drenador de corriente constante).
Se parte de I = C x dV / dt, considerando descarga a corriente constante. Por lo tanto, la forma de la tensión sobre las placas del condensador de filtro va a ser un segmento de recta con pendiente decreciente con el tiempo (algo como esto -> \ ).
Aquí dV pasa a ser Vpp
dt pasan a ser esos milisegundos citados (tener presente cuándo es rectificación de media onda o cuándo es rectificación de onda completa, porque los milisegundos cambian)
I es la corriente media de carga (que pasa a ser igual a la corriente de descarga).
Suele dar resultados aproximados y, por lo general, la capacidad resultante es mayor a la necesaria si el dt tomado se aproxima al tiempo de medio ciclo (ejemplo: 10 mseg para rectificación de onda completa con frecuencia de línea de 50 Hz). Con 7 mseg, estimo que se contempla casos más frecuentes y reales de ripple (aunque no comparé los resultados con métodos más complejos de cálculo).
Dispongo de un desarrollo matemático un poco más complejo para calcular la capacidad teniendo en cuenta el porcentaje de ripple deseado. Lo hice hace muchos años, cuando lo encuentre lo subo. No emplea este método sino funciones coseno, seno y ln. Sigue siendo aproximado también, solo que la aproximación no se hace en la forma de la descarga sino en la relación que guarda los picos de ripple con el valor medio de tensión entre placas.
Saludos
Aquí va el desarrollo matemático:
Rectificación de media onda:
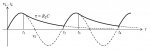
Si consideramos diodos rectificadores y transformadores ideales, t1 va a coincidir con el centro del primer semiciclo de la figura (en la figura no se indica exactamente eso, ya que fue “rescatada” de un libro para evitarme dibujarla en detalle). Esto es en 5 mseg después del origen del eje t, para una frecuencia de línea de 50 Hz. En t1 se va a dar VLMÁXIMA (o VM, para sintetizar de aquí en más).
t2 va a estar definido por el conjunto de RL y C, que son la carga y el condensador de filtro, respectivamente. Su ubicación, por lo general y en la práctica, va a ser entre los 20 mseg y los 25 mseg de esa misma figura (es decir, en algún lugar de la primera cuarta parte del segundo ciclo del voltaje de secundario). Aclaración: t2 puede ubicarse por debajo de los 20 mseg (en esta figura específica) bajo determinadas condiciones de RL y C (valores extremadamente bajos de uno, de otro o de ambos parámetros, por ejemplo). Nosotros vamos a tomar t2 entre los 20 y los 25 mseg (que resulta el caso más racional). En t2 se va a dar VLmínima (o Vm, para sintetizar de aquí en más).
Después de sucesivas operaciones matemáticas (con las que no vienen al caso complicarnos más):
C = ( arco coseno ( Vm / VM ) – 2 . Π ) / ( 2 . Π . 50 . RL . LN ( Vm / VM ))
Válida para 50 Hz de frecuencia de línea. LN: base de los logaritmos neperianos. Yo solía utilizar una vieja calculadora científica CASIO fx100C en modo 5 (RAD), para efectuar este cálculo.
Vm / VM suele tomar valores de menos de 1: 0,90 a 0,97 suelen ser comunes.
Ejemplo: RL = 1000 ohmios y Vm / VM = 0,99 (ripple muy exigente)
C = 1945,16 uF
Del mismo modo, pero para Rectificación de onda completa:
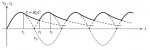C = arco coseno ( - Vm / VM ) / ( - 2 . Π . 50 . RL . LN ( Vm / VM ))
Válida para 50 Hz de frecuencia de línea. Atención a los dos signos menos!!!.
Ejemplo: RL = 1000 ohmios y Vm / VM = 0,99 (ripple muy exigente)
C = 950,16 uF
Así como están dadas las fórmulas se pueden utilizar, pero por tanteo y teniendo bastante experiencia, pero para que sean aplicables por todos y sin contar con mucha experiencia vamos a avanzar un poquito más todavía.
Ahora, entra en juego el factor de rizado para ambas fórmulas (Fr):
Fr = Vr eficaz / Vo
Donde Vr eficaz es el voltaje de rizado eficaz que se “monta” sobre el valor medio de tensión de salida Vo.
Vo es un dato de partida para el diseño de nuestra fuente.
Podemos relacionar Vr eficaz con Vo y aquí viene mi única aproximación: supongo la forma de onda del ripple como si fuera verdaderamente senoidal pura (en rigor, no lo es).
Entonces, hago Vr pico / raiz ( 2 ) (que es propio de señales senoidales puras) y vinculo Vr pico a Vo como una fracción de Vo.
Queda:
Vr pico = p . Vo, siendo p la fracción correspondiente.
Entonces, Fr = p . Vo / ( Vo . raiz ( 2 )) = p / raiz ( 2 )
p = Fr . raiz ( 2 )
Ejemplo:
si Fr = 0,01 (esto representa un 1% de ripple)
p = 0,01 . raiz ( 2 ) = 0,01414213...
Surgen:
VM = Vo + p . Vo = Vo ( 1 + p )
Vm = Vo – p . Vo = Vo ( 1 – p )
Vo = VM / ( 1 + p ) = Vm / ( 1 – p )
Vm / VM = ( 1 – p ) / ( 1 + p )
Válido para ambos tipos de rectificación.
Sólo resta fijar Fr en algún valor conveniente (digamos entre el 1% y el 3%), calcular p y obtener en consecuencia Vm / VM y luego C.
Tengo tablas de C para distintos valores de Fr y RL. Cuando las encuentre, las subo.
Aclaración: este es un método que se me ocurrió aplicar cuando iva al secundario y me pareció interesante compartir, dado que no lo he visto analizado de esta forma. En esa época nos habían explicado las curvas de Don Schade, pero me carcomía conocer cómo el tipo las había obtenido. Es por eso que me puse a renegar para "llegar" con un método propio!!!. Las ecuaciones de C son exactas y tienen en cuenta una descarga exponencial decreciente en el voltaje del condensador de filtro, gracias a la idealización de los diodos y del transformador.
