Curso sobre Cuaterniones para la rotacion y orientación

[Nepper]

Buenas!
Primero que todo. Una masa el sistema autómatico de busqueda del foro cuando colocas el titulo.

Voy a preguntar un tema mas bien matematico, no tanto electrónico. Estoy trabajando con robots industriales, y estos utilizan un sistema de referencia para moverse. La punta del robot (el punto de referencia movil, que utilizaremos para mover la herramienta que maneja el robot) la llamaremos TCP.
Este punto en el espacio tridimensional, no solo tiene una posición en X, Y y Z, si no que además se le deben definir 4 cuaternios, q1, q2, q3 y q4.
Los cuaternios los utiliza para indicarle al robot, la rotación y orientación que posee el TCP

Una herramienta con sus puntos recorridos:

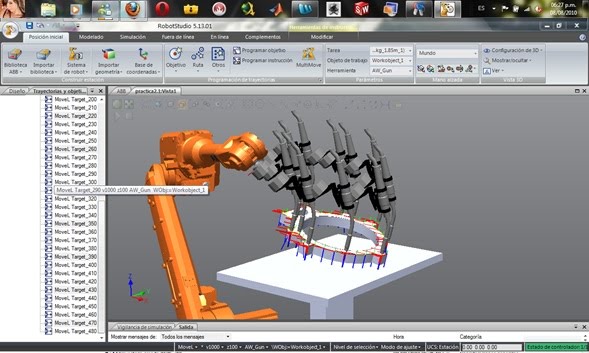
Definición de TCP:

¿Que sucede? yo quiero definir un nuevo TCP. Justamente, mi herramienta será una torcha de soldadura MIG

Imaginen, que la punta de esa torcha, se encuentra a 100mm en Y, a 0 en X y a -50 en Z {100,0,-50}respecto de la punta del robot (sin herramienta).
Pero existe un problema. Yo quiero que la dirección de la tobera, sea el eje Z. Si se me ocurre subirlo (moverlo en Z), el robot tiene que moverse de tal forma que la tobera suba o baje siempre a 45º (segun el caso de la foto). Pero si yo pongo la tobera a 90º respecto al suelo, la tobera tiene que subir y bajar como si fuera el eje Z real. ¿se entiende?

El problema ocurrió cuando quise definir un nuevo TCP. Le asigné el X, Y, Z correspondientes, pero a la hora de definir los cuaternios, este me daba falla. Basicamente, no se geometricamente que estoy haciendo poniendole numeros a los cuaternios.

Estuve investigando, y en la wikipedia explica la rotación y orientación de los cuaternios, pero no puedo relacionarlo con los 4 parametros que me pide el robot.
Estuve buscando sobre ellos, y note que se utiliza mucho en computación, vi videos en youtube pero nada dice como paso de la definición a los 4 que necesita el robot.

Pude ver que 1 cuaternio consta de 4 numeros, es como un numero complejo, pero con 4 terminos.
El numero complejo, pongo su valor en X para los reales y Y para los complejos, y obtengo el vector del cual puedo calcular su modulo y angulo, ¿pero en el cuaternio como hago?

Supongan que hago 0 al valor real del cuaternio, se que obtengo las coordenadas en x, y, z de mi vector. q=0+ a i + b j + c k. Pero no obtengo la rotación... bueno, no la veo!

Al momento de hacer interpretaciones geométricas, Hamilton se dio cuenta que haciendo que la parte real fuera igual a cero, las tres unidades imaginarias podían representar muy cómodamente los puntos en el espacio, y después identificó sus propiedades rotacionales. (http://www.oocities.org/ricardo_arturo/cuatern/hist.htm)

¿Alguien sabe bien como visualizar los cuaternios y como interpretarlos en el espacio? O sea, ¿Como se que numeros me indican que rotación y orientación?

Tema jodido, pero gracias por leer por lo menos

PS: la barra de inicio de la primer imagen NO es de mi computadora u_u

 

[chclau]

Hasta hace un anio atras yo estuve usando una herramienta gratuita para programar juegos y simulaciones en 3D que se llama Unity3D, y que casualmente tambien utilizaba cuaterniones para la definicion de coordenadas de rotacion. La ventaja en el caso de Unity es que ya tenia funciones incorporadas para generar cuaterniones a partir de angulos de Euler.

Pero me parece un poco mucho que te instales esa herramienta solo para calcular cuaterniones, asi que busque un poco por Google y encontre esto, fijate si ta ayuda

http://www.flipcode.com/documents/matrfaq.html#Q47

 

[chclau]

Agrego una pequenia aclaracion que se me quedo en el tintero. Me parece que es imposible visualizar los cuaterniones, son entidades matematicas que dan ciertas ventajas para realizar calculos de rotacion pero no tienen ninguna relacion directa con la realidad fisica. Algo asi como las frecuencias negativas, que tambien usamos pero solamente porque son faciles de manipular matematicamente, sin que tengan ninguna correlacion con la realidad.

Para visualizar los cuaterniones los tenes que reconvertir a coordenadas de rotacion en 3D.

 

[Nepper]

Ha!! Te entendi muy bien...
Lo digo en serio....
Entonces solo tengo que encontrar las ecuaciones de conversion a grados de euler....

Despues lo veo al software, es que estoy con otros problemitas...

Muchas gracias!

 

[Eduardo]

...¿Alguien sabe bien como visualizar los cuaternios y como interpretarlos en el espacio? O sea, ¿Como se que numeros me indican que rotación y orientación?

Empecemos por su forma más simple: 4 coordenadas y módulo 1.
O sea: Qr = ix+jy+kz+w = w+V (V:vector , w:escalar)
La fórmula de rotación es q' = Qr*·q·Qr (Qr* el cuaternión conjugado)

¿Como vemos en el espacio a Qr?
Muy simple: El vector V coincide con el eje de la rotación y |V|/w la tangente del ángulo girado sobre 2.

Entonces, si el problema es: Dado un eje E (vector de módulo 1) queremos rotar un ángulo alfa --> el cuaternión correspondiente será Qr = sen(alfa/2)·E + cos(alfa/2)



El resto es trabajar sobre lo mismo y dependerá del sofware como entregarle el cuaternión así como el sentido del ángulo girado.

Por ejemplo, el software puede hacer la rotación aplicando q' = (Qr*·q·Qr)/(Q*·Qr)
que elimina la necesidad que el módulo de Qr sea 1.
La interpretación sigue siendo la misma: La parte vectorial coincide con el eje de rotación y |V|/w = tan(alfa/2).

También el soft puede aplicar esta última fórmula, asumir que la parte escalar es 1 y usar (o no) la 4ta coordenada para otra cosa.

 

[morta]

Fijate si te sirve algo del capitulo de "espacios vectoriales" del libro de algebra lineal grossman.

 

[Nepper]

Buenas!
La cosa que no me olvidé del tema.. lo estoy digeriendo de a poco... cayo pesado..
Me encontré con la wiki en ingles muy bien explicado
http://en.wikipedia.org/wiki/Quaternions_and_spatial_rotation
Sin duda, la cosa me ayudó cuando entendí el problema que se intentaba resolver con los cuaterniones
el Gimbal Lock
http://en.wikipedia.org/wiki/Gimbal_lock

no... es... otra cosa....
O sea, mi problema es saber que le tengo que poner a las 4 variables para que me quede apuntando para abajo y con la rotación que quiero.
Hasta ahora entiendo que con esto (q' = Qr*·q·Qr) lo que se hace es encontrar la "función" rotación para una rotación definida.
Es como derivar, no encontrás el resultado numerico, solo la función derivada que luego analizarás.

Mi otro problema, fue no entender los tecnisismos. Tambien falta de interpretación en las matemáticas y sistemas de coordenadas.
Se puede indicar una orientación y rotación de 2 maneras:
Angulos de euler: Se utilizan solo 3 ejes (solo 3 angulos) que indican que inclinación posee cada ejer respecto del origen. De esta forma se puede saber la rotación de cada plano y del vector resultante.
http://en.wikipedia.org/wiki/Euler's_rotation_theorem
Sistema de 3 coordenadas y rotación del vector: En este sistema, se especifica un punto en 3D, y luego se especifica un angulo. Este angulo es la rotación del vector (siendo el vector el eje de rotacion). Basicamente, es la representación gráfica de un numero complejo en 3D (tal como se define el cuaternion).
http://en.wikipedia.org/wiki/Axis-angle_representation

Sin duda, estos no son los parámetros que me pide el robot... seguiré investigando...

Bueno... hay cosas raras... tienen sentido....

Despues de leerme un rato la wiki... recordé el link de chclau

Hasta hace un anio atras yo estuve usando una herramienta gratuita para programar juegos y simulaciones en 3D que se llama Unity3D, y que casualmente tambien utilizaba cuaterniones para la definicion de coordenadas de rotacion. La ventaja en el caso de Unity es que ya tenia funciones incorporadas para generar cuaterniones a partir de angulos de Euler.

Pero me parece un poco mucho que te instales esa herramienta solo para calcular cuaterniones, asi que busque un poco por Google y encontre esto, fijate si ta ayuda

http://www.flipcode.com/documents/matrfaq.html#Q47

me encontré con esto:

Q56. How do I convert a rotation axis and angle to a quaternion?
----------------------------------------------------------------
Given the rotation axis and angle, the following algorithm may be used to generate a quaternion:
------------------------------------------------
sin_a = sin( angle / 2 )
cos_a = cos( angle / 2 )
q -> x    = axis -> x * sin_a
q -> y    = axis -> y * sin_a
q -> z    = axis -> z * sin_a
q -> w    = cos_a
quaternion_normalise( q );
------------------------------------------------
It is necessary to normalise the quaternion in case any values are very close to zero.

Principalmente, esto es lo que necesito.. pero lo seguiré investigando y entendiendo que robots estoy haciendo...



claro! ahora entiendo otra cosa... en realidad, yo siempre pensé en rotación en los tres ejes, pensé que eso era lo mas cómodo para definir la orientación y rotación de la herramienta ya que solo debía rotarla en 0º, 45º y 0º. Pero si me lo pongo a ver, puede no ser mas sencillo, pero tampoco mas complicado. Defino un punto a 45º ascendente en el plano X, Z del eje y rotación 0º del vector, o sea, las coodenadas (el largo del vector no importa (módulo)) 1, 0, 1 con un angulo de rotación 0º. Eso me dará un angulo con respecto al eje X de 45º, y con respecto al eje Z 45º, pero como 0 en la coordenada Y, este punto no se mueve del plano X Z.
Esto me daría el mismo resultado que el anterior mencionado. La diferencia es que dicho de la 2da forma, vector y angulo, puedo pasarlo facilmente a los cuaterniones (forma binomial del cuaternion por asi llamarlo)

No tengo el sketchup, despues subo una imagen 3D para apoyar esto último.



claro!! y despues lo normalizo para que el largo del vector sea 1 y así me lo pueda tomar el robot!!!!