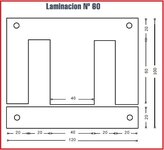
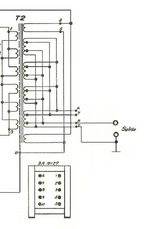
En realidad para los 8 Ohm deseados deberíamos tener unas salida de 23,5 Volts
por lo que la de 20 Volts es la mas aproximada y nos da 5,8 Ohms ( 20 x 20) /5,8 = 68,9 Watts)
De la forma que lo armé yo, en la salida de 30 Volts la impedancia es de 13 Ohms , la cual se aproxima a 16 Ohms para dos parlantes de 8 Ohms en serie, esto sería entre los terminales 6 y 7 del transformador de salida, yo pondría la 7 a tierra y usaría la 6 de salida.
Aunque parezca que suena, y funciona bien, no es así, si bien en números 5,8 Ω , parece cerca de 8 Ω, y 13 Ω parece cerca de 16 Ω, en realidad está muy alejados, veamos porqué :
Como en este amplificador se desconoce la resistencia de carga de placa a placa (Raa), le daremos un valor arbitrario, pero cercano, y correspondiente a un push-pull- paralelo con 4 pentodos de potencia EL36, y 70 W R.M.S. clase AB, que podría estar entre los 2.500 Ω, y 3.000 Ω, eligiremos
2.500 Ω.
Para que cualquier amplificador a válvulas funcione correctamente, siempre se debe mantener el valor de la resistencia de carga, y en este caso por ser push-pull, de placa a placa (Raa).
La resistencia de carga de placa a placa del primario, es reflejada por la impedancia de la bobina móvil a conectar en el secundario, quiere decir que si conectamos al secundario una bobina móvil de distinta impedancia a la que corresponde, esta hará variar la resistencia de carga de placa a placa en el primario, esto aunque no se note al oído, corre el punto de trabajo de la línea de carga, generando distorsión, cambiando el porcentaje de disipación de las placas de las válvulas de salida, y que cuando se corre el punto de trabajo de la línea de carga, se alteran casi todos los parámetros de la etapa de potencia.
Veamos lo que sucede al variar el valor de las bobinas móviles respecto del valor correcto.
A la resistencia de carga de placa a placa (Raa), la llamaremos :
Z1
A la bobina móvil la llamaremos :
Z2
A la relación de transformación la llamaremos:
k
Para conocer el nº de espiras de un secundario para cargar una bobina móvil
(Z2), hay que hallar la relación de transformación
(k).
k =

Z1/Z2
Si Z1 es
2.500 Ω, y Z2 es
5,8 Ω, k =  2.500 Ω / 5,8 Ω = 20,76
2.500 Ω / 5,8 Ω = 20,76, entonces
k = 20,76 relación de transformación que es inalterable, dado por el número de espiras del primario, y del secundario.
Ahora veamos que sucede con la resistencia de carga de placa a placa (Raa) (Z1), conectando en el secundario una bobina móvil distinta de 5,8 Ω, para este caso de 8 Ω.
Si
k = Z1/Z2,
Z1/Z2, entonces
Z1 = (k^2) Z2 = (20,76^2) 8 Ω =
3.448 Ω
Podrán apreciar que la resistencia de carga de placa a placa (Raa) (Z1) varió dramáticamente de 2.500 Ω a 3.448 Ω con cambiar una bobina móvil de 5,8 Ω a otra de 8 Ω.
Para el 2do caso corresponde conectar al secundario una bobina móvil de 13 Ω, veremos que sucede lo mismo que en el caso anterior si conectamos otra bobina móvil de valor distinto, y de 16 Ω
Veamos:
k=

Z1/Z2 =

2.500 Ω/13 Ω : k= 13,87, entonces
k = 13,87 relación de transformación que es inalterable, dado por el número de espiras del primario, y del secundario.
Si
k =  Z1/Z2,
Z1/Z2, entonces
Z1 = (k^2) Z2 = (13,87^2) 16 Ω =
3078 Ω
Aquí también la resistencia de carga de placa a placa (Raa) (Z1) varió dramáticamente de 2.500 Ω a 3.078 Ω con cambiar una bobina móvil de 13 Ω a otra de 16 Ω.
Saludos Cordiales
Rorschach