Duda con circuito RC

[cosmefulanito04]

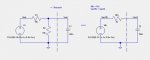
Si supones que R*C<<<Ton y Toff, podes suponer que la entrada es un escalon y aplicar de una Laplace (no sabia que este foro tenia Latex, eso esta bueno ).

[LATEX]H(s)=\frac{1000}{s+2000}

V(s)=\frac{Vcc}{s}

Vo(s)=\frac{Vcc*1000}{s*(s+2000)}

Residuos:

\lim_{s \rightarrow \0} \frac {s*1000*Vcc}{(s+2000)*s}=\frac{Vcc}{2}


\lim_{s \rightarrow \(-2000)} \frac {(s+2000)*1000*Vcc}{(s+2000)*s}=\frac{-Vcc}{2}

Vo(s)=\frac{Vcc/2}{s}-\frac{Vcc/2}{(s+2000)}

vo(t)=Vcc/2*u(t)-Vcc/2*e^{-2000*t}*u(t)

vo(t)=Vcc/2*(1-e^{-2000*t})*u(t)
[/LATEX]

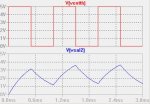
Esto partiendo de la 1era suposicion (debemos pensar que la señal es periodica), si analizamos a 100Hz el periodo sera 10mSeg, y R*C=1mSeg, con lo cual si Ton=Toff estas justo en 5tao, con lo cual la aproximacion es buena y la salida sera una señal periodica con la forma que se obtuvo con un escalon. A medida que la frecuencia aumente, esta aproximacion ya no sirve.

Ahora como obtuviste esas expresiones para obtener el max. y el minimo, ni idea.

 

[Eduardo]

Esto era asi:

Primero le pegamos una simplificación al circuito para poder usar resultados conocidos.
En este caso, pide a gritos el teorema de Thevenin (1er imagen) y queda el típico problema de carga de un capacitor a través de una resistencia.


La expresión general (incluye las condiciones iniciales) de la tension de salida en ese circuito es:

[LATEX]Vsal(t) = Vini\;e^{-\frac{t}{Rth\;C}}\;+\;V\infty(1-e^{-\frac{t}{Rth\;C}})[/LATEX]
​

La evolución de la tensión será como en la imagen siguiente:


- En el 1er intervalo será V∞=Vcc/2=5V y Vini=0
- En el 2do V∞=0 y Vini= la tensión final del 1er intervalo.
- En el 3ero V∞=Vcc/2=5V y Vini= la tensión final del 2do intervalo
- etc

Pasado el período transitorio, los valores máximo y mínimo que alcance la tensión serán siempre los mismos.
Entonces, usando la expresión general:

[LATEX]Vsal_{max} = Vsal_{min}\;e^{-\frac{T}{Rth\;C}}\;+\;\frac{Vcc}{2}\;(1-e^{-\frac{T}{Rth\;C}})
Vsal_{min} = Vsal_{max}\;e^{-\frac{T}{Rth\;C}}[/LATEX]
​

con T=1/(2f) la duración de cada intervalo.

De ahí, con un poco de álgebra y recordando que Rth=R/2 , se llega a las expresiones:

[LATEX]Vsal_{min} = \frac{Vcc/2}{1+e^{\frac{1}{f\;R\;C}}}\;\; ;\;\; Vsal_{max} = \frac{Vcc/2}{1+e^{-\frac{1}{f\;R\;C}}}\;\; ;\;\;Vpap=Vcc/2\;Tanh(\frac{1}{2\;f\;R\;C})[/LATEX]​

 

[cosmefulanito04]

Es algo parecido a lo que puse, pero en mi caso solo lo limite a R*C<<<Ton y Toff, con lo cual Vmax=Vcc/2 y Vmin=0, en caso de que 5*R*C>Ton y Toff, ahi empiezo a tener esa condicion inicial que pusiste que hace que la señal quede levantada como graficaste.

 

[unmonje]

Esto era asi:

Primero le pegamos una simplificación al circuito para poder usar resultados conocidos.
En este caso, pide a gritos el teorema de Thevenin (1er imagen) y queda el típico problema de carga de un capacitor a través de una resistencia.

Ver el archivo adjunto 44814
La expresión general (incluye las condiciones iniciales) de la tension de salida en ese circuito es:

[LATEX]Vsal(t) = Vini\;e^{-\frac{t}{Rth\;C}}\;+\;V\infty(1-e^{-\frac{t}{Rth\;C}})[/LATEX]
​

La evolución de la tensión será como en la imagen siguiente:

Ver el archivo adjunto 44815
- En el 1er intervalo será V∞=Vcc/2=5V y Vini=0
- En el 2do V∞=0 y Vini= la tensión final del 1er intervalo.
- En el 3ero V∞=Vcc/2=5V y Vini= la tensión final del 2do intervalo
- etc

Pasado el período transitorio, los valores máximo y mínimo que alcance la tensión serán siempre los mismos.
Entonces, usando la expresión general:

[LATEX]Vsal_{max} = Vsal_{min}\;e^{-\frac{T}{Rth\;C}}\;+\;\frac{Vcc}{2}\;(1-e^{-\frac{T}{Rth\;C}})
Vsal_{min} = Vsal_{max}\;e^{-\frac{T}{Rth\;C}}[/LATEX]
​

con T=1/(2f) la duración de cada intervalo.

De ahí, con un poco de álgebra y recordando que Rth=R/2 , se llega a las expresiones:

[LATEX]Vsal_{min} = \frac{Vcc/2}{1+e^{\frac{1}{f\;R\;C}}}\;\; ;\;\; Vsal_{max} = \frac{Vcc/2}{1+e^{-\frac{1}{f\;R\;C}}}\;\; ;\;\;Vpap=Vcc/2\;Tanh(\frac{1}{2\;f\;R\;C})[/LATEX]​

Exelente aporte....!!!!
A parte de ti, quien mas usa estos càlculos en Santo Tomè ???

 

[Eduardo]

Aparte de ti, quien mas usa estos càlculos en Santo Tomè ???

Es un ejercicio de Teoría de Circuitos, no creo que le sirva a un estudiante de cocina.