Acá encontré algo como para mirar. Yo lo estoy leyendo aún.
http://bibliotecadigital.ilce.edu.mx/sites/ciencia/volumen2/ciencia3/106/htm/sec_5.htm
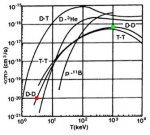
En la figura 5 está la curva de la probabilidad de fusion D-D por unidad de tiempo, que da una idea del rendimiento del reactor según la temperatura del plasma.
Reproduzco aquí la curva para los que no quieren leerse todo el asunto.
Según la curva conviene trabajar a T = 1 MeV para obtener la máxima producción de reacciones.
Digo "según" porque con estas cuentas hay que andar con cuidado: si la curva se obtuvo luego de integrar la sección eficaz de fusión D-D para una maxwelliana, entonces el resultado es aproximado. La maxwelliana presupone solamente colisiones elásticas, y las colisiones que conducen a fusión son inelásticas. El plasma en equilibrio debe coexistir con ellas, y encima uno desea maximizarlas.
La solución exacta del problema se encuentra resolviendo la ecuación de Boltzmann, con reacciones de fusión[1] (y ya nos acercamos al Megombo !!!). Para algunos casos simples, pero con procesos inelásticos presentes, la función distribución en equilibrio no se parece en nada a la maxwelliana[2].
Entonces: ¿ qué hacemos ?
Pues por ahora nos quedamos con el resultado maxwelliano solamente como una estimación preliminar.
¿ Cómo se usa el resultado de la gráfica ?
En el punto máximo da aprox. Secc Eficaz D-D = 8E-17 cm3/seg.
Si se multiplica la Secc. Eficaz D-D por la concentración de iones que se tiene en el reactor, digamos: n = 1E20 cm-3, se obtiene la tasa de reacciones máxima esperable:
Tasa de fusión D-D = 8000 reacciones por segundo (para n = 1E20 cm-3 y T=1 MeV).
Eso es el máximo !!! Las deficiencias del reactor pueden tirar abajo ese número. Ahí es donde entra a jugar el diseño (la muñeca del artista).
Finalmente todo depende de la concentración y temperatura que se logre en el plasma.
Y esto dependerá de la eficiencia del confinamiento y calentamiento del reactor de Farsworth.
Ánimo !!!
Referencias:
[1] Datos de secciones eficaces reales: http://www.cientificosaficionados.c...?p=25761&sid=edee54143ef29b93e2c5c6f88aacd0aa
[2] Ferreira, C. M. "Current Research Topics in Low-Pressure Glow Discharges in Rare Gases and Pure Nitrogen. Ed. Erich E. Kunhardt and Lawrence H. Luessen, (fecha no disponible).
PD:
Yo en el ejemplo usé n=1E20 cm-3. Para comparar con la concentración de partículas a presión atmosférica, podemos calcular que en 1 mol hay 6E23 partículas (6x10^23), y que ocupan 22,4 litros (22,4 dm3 = 22400 cm3). O sea que a nivel del mar y en CNTP:n0 ~ 6E23/2,24E4 partíc/cm3 => n0 ~ 3E20 cm-3.
http://bibliotecadigital.ilce.edu.mx/sites/ciencia/volumen2/ciencia3/106/htm/sec_5.htm
En la figura 5 está la curva de la probabilidad de fusion D-D por unidad de tiempo, que da una idea del rendimiento del reactor según la temperatura del plasma.
Reproduzco aquí la curva para los que no quieren leerse todo el asunto.
Según la curva conviene trabajar a T = 1 MeV para obtener la máxima producción de reacciones.
Digo "según" porque con estas cuentas hay que andar con cuidado: si la curva se obtuvo luego de integrar la sección eficaz de fusión D-D para una maxwelliana, entonces el resultado es aproximado. La maxwelliana presupone solamente colisiones elásticas, y las colisiones que conducen a fusión son inelásticas. El plasma en equilibrio debe coexistir con ellas, y encima uno desea maximizarlas.
La solución exacta del problema se encuentra resolviendo la ecuación de Boltzmann, con reacciones de fusión[1] (y ya nos acercamos al Megombo !!!). Para algunos casos simples, pero con procesos inelásticos presentes, la función distribución en equilibrio no se parece en nada a la maxwelliana[2].
Entonces: ¿ qué hacemos ?
Pues por ahora nos quedamos con el resultado maxwelliano solamente como una estimación preliminar.
¿ Cómo se usa el resultado de la gráfica ?
En el punto máximo da aprox. Secc Eficaz D-D = 8E-17 cm3/seg.
Si se multiplica la Secc. Eficaz D-D por la concentración de iones que se tiene en el reactor, digamos: n = 1E20 cm-3, se obtiene la tasa de reacciones máxima esperable:
Tasa de fusión D-D = 8000 reacciones por segundo (para n = 1E20 cm-3 y T=1 MeV).
Eso es el máximo !!! Las deficiencias del reactor pueden tirar abajo ese número. Ahí es donde entra a jugar el diseño (la muñeca del artista).
Finalmente todo depende de la concentración y temperatura que se logre en el plasma.
Y esto dependerá de la eficiencia del confinamiento y calentamiento del reactor de Farsworth.
Ánimo !!!
Referencias:
[1] Datos de secciones eficaces reales: http://www.cientificosaficionados.c...?p=25761&sid=edee54143ef29b93e2c5c6f88aacd0aa
[2] Ferreira, C. M. "Current Research Topics in Low-Pressure Glow Discharges in Rare Gases and Pure Nitrogen. Ed. Erich E. Kunhardt and Lawrence H. Luessen, (fecha no disponible).
PD:
Yo en el ejemplo usé n=1E20 cm-3. Para comparar con la concentración de partículas a presión atmosférica, podemos calcular que en 1 mol hay 6E23 partículas (6x10^23), y que ocupan 22,4 litros (22,4 dm3 = 22400 cm3). O sea que a nivel del mar y en CNTP:n0 ~ 6E23/2,24E4 partíc/cm3 => n0 ~ 3E20 cm-3.
Adjuntos
Última edición: